Kvantummechanikai atommodell

Schrödinger dolgozta ki az említett matematikai atommodellt. Az atompályát (is) jellemzik benne bizonyos kvantumszámok.

főkvantumszám
mellékkvantumszám
mágneses kvantumszám

Ezek az atompályákat jellemzik. Van egy negyedik:

spinkvantumszám

Ez szoros összefüggésben van a Pauli-elvvel, mely szerint egy atompályára maximálisan kettő, ellentétes spinű elektron kerülhet. A spin csak kétféle lehet, lefelé és felfelé mutathat. Ez a két irány azt jelzi, hogy hogyan helyezkednek el az elektronok a külső mágneses térhez viszonyítva. Két állapot van tehát.

Az irányoknak természetesen jelentése is van – amikor fölfelé irányt vesz, akkor ugyanolyan irányú, mint a külső mágneses tér.

Ha lefelé irányt vesz fel, akkor ellentétes irányú a külső mágneses térhez viszonyítva az elektron elhelyezkedése.

Tulajdonképpen ez egy mágnestűként is elképzelhető, csak nagyon kicsiben és elektronokra vonatkoztatva.

A spinkvantumszám értéke nem egész szám – eltérően a többi kvantumszámtól. Csak két értéket vehet fel: +1/2;-1/2

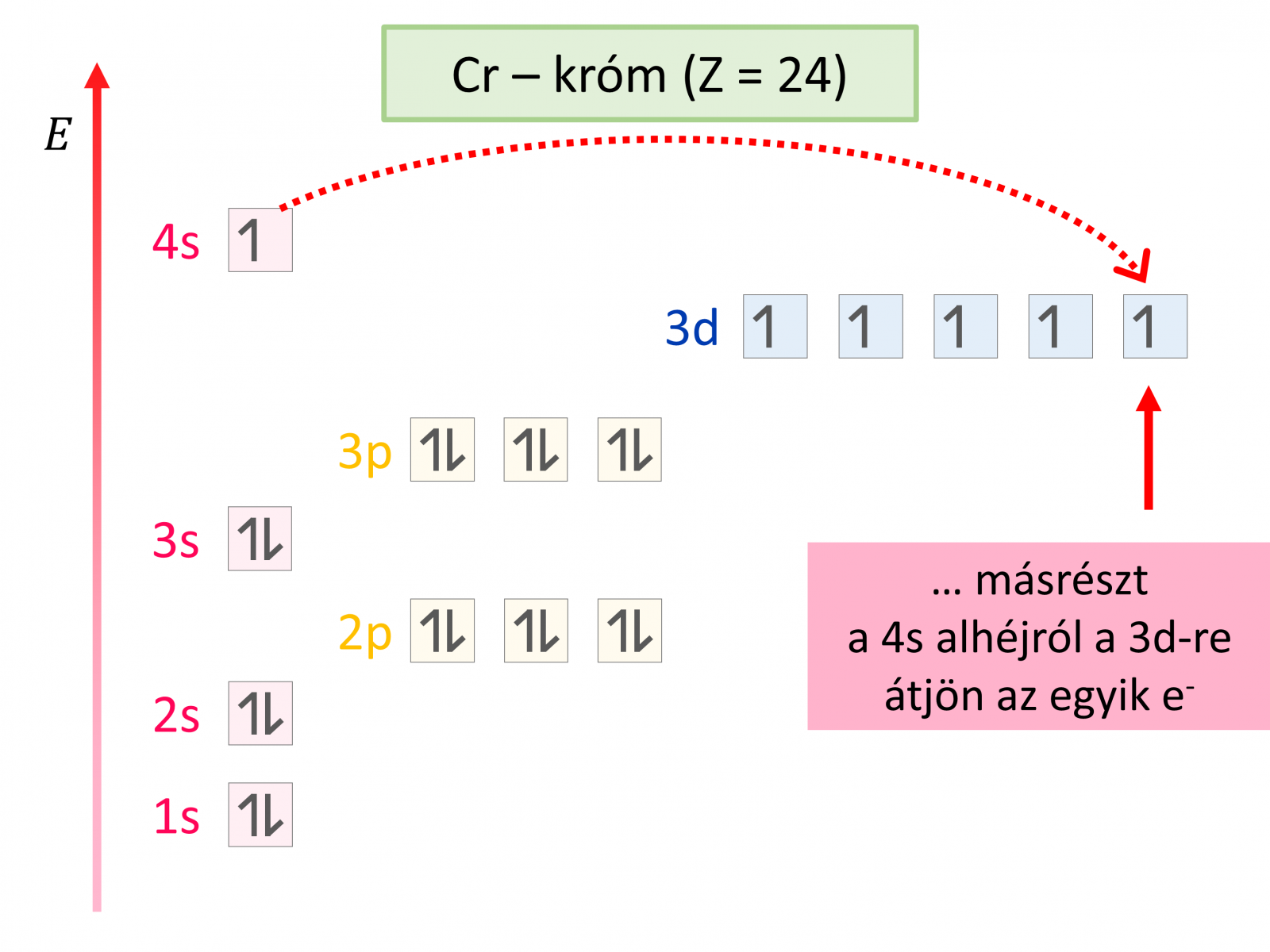
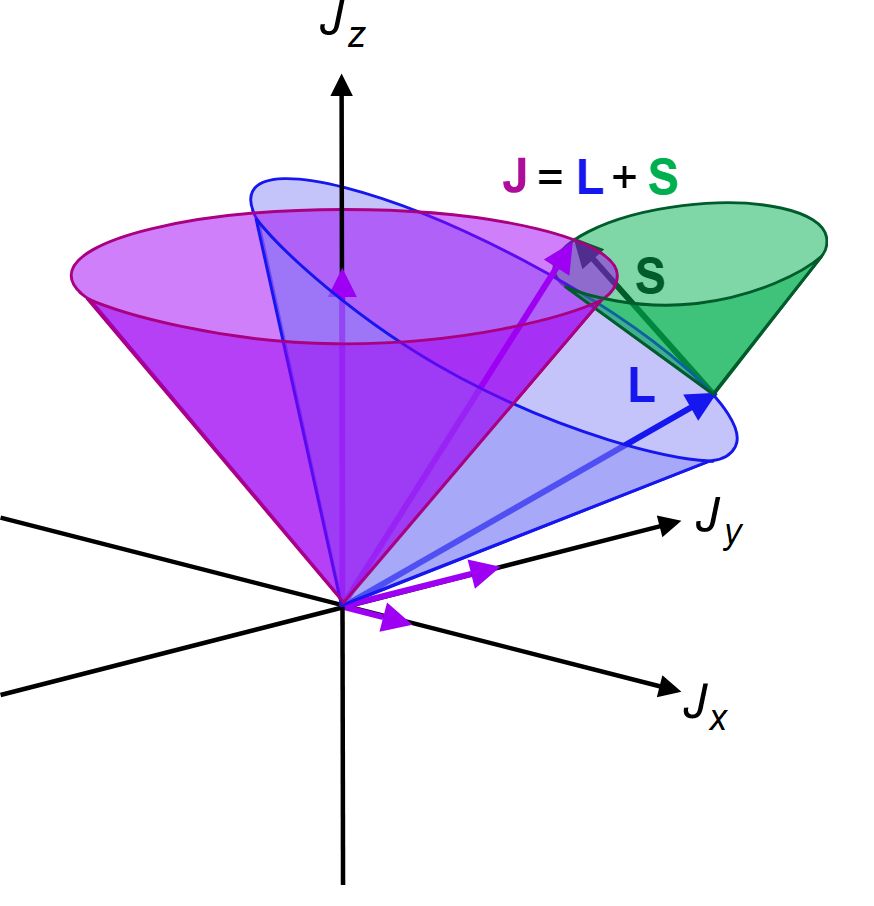
Úgy is meg lehet fogalmazni, hogy a spinkvantumszám az elektron sajátperdületének kitüntetett irányú vetületét adja meg. (Ez a Z tengely iránya). Az elektron sajátperdülete mindig ugyanakkora, illetve az elektron teljes perdülete (J): a pályaperdület (L) és a sajátperdület (S) összege.

Néhány szó a fő-, mellék,- mágneses kvantumszámokról:

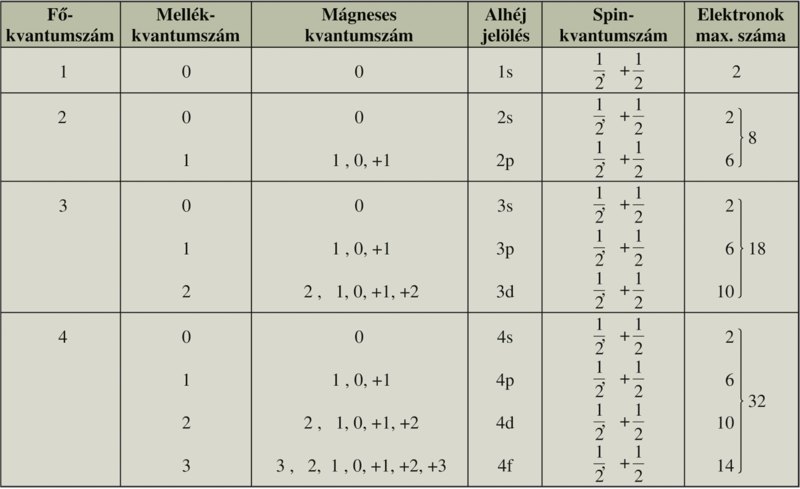
Főkvantumszám: (n)

Azok az atompályák tartoznak egy héjba, amelyeknek ugyanolyan a főkvantumszámuk.

K-tól kezdődik a jelölésük, nagybetűkkel. (K,L,M,N,O). Minél nagyobb a főkvantumszám értéke, annál nagyobb méretű pályáról beszélünk.

Mellékkvantumszám: (l)

Azok a pályák tartoznak egy alhéjba, melyeknek ugyanaz a mellékkvantumszámuk. s-től kezdődik a jelölésük, kisbetűkkel. (s,p,d,f). Minél nagyobb szám jelöli a mellékkvantumszámot, annál összetettebb az adott pálya szimmetriája.

A fő-és mellékkvantumszámtól függ a pályaenergia!

Mágneses kvantumszám: (m)

Megadja, hogy mágneses térbe helyezett atom atompályái hogyan helyezkednek el, a mágneses erővonalakhoz viszonyítva. Értékére hatással van a mellékkvantumszám értéke.

Hogyan?

-l, (-l+1), -l+2, … 0, … l-2, l-1, l

Ez nagyon rosszul hangzik, de nem annyira bonyolult:

Az l a mellékkvantumszám jele. s,p,d,f alhéjakról beszélünk mellékkvantumszám esetén.

A fent megadott számítás alapján:

s-alhéj: (itt l=0) tehát, a mágneses kvantumszám nem lehet csak nulla àm=0

p-alhéj: (itt l=1) tehát, a mágneses kvantumszám: -1,0,+1 (csak be kell helyettesíteni az 1-et a kiemelt képletbe)

d-alhéj: (itt l=2) tehát, a mágneses kvantumszám: -2,-1,0,1,2

f-alhéj: (itt l=3) tehát, a mágneses kvantumszám: -3,-2,-1,0,1,2,3

Mágneses kvantumszám alapján következtethető:

egyféle s-pálya van
háromféle p-pálya van
ötféle d pálya-van
hétféle f pálya-van

Miért?

A mágneses kvantumszám, a megbeszéltek szerint az atompályák külső mágneses térben való viselkedését befolyásolja, a mágneses kvantumszámra pedig a mellékkvantumszám hat – az pedig a pályaszimmetriát határozza meg. A főkvantumszám + mellékkvantumszám pedig a pályaenergiát határozzák meg.

Megjegyzés:

Láttuk, hogy a spin-, és mágneses kvantumszám is külső mágneses térhez megadott viszonyrendszert tisztáz. A különbség az, hogy a spinkvantumszámnál magukról az elektronokról beszéltünk, a mágneses kvantumszám esetében pedig az atompályákról, ebben a vonatkozásban.

Min alapszik a kvantummechanikai atommodell?

Alapjait azok a tapasztalatok képezik, miszerint egy adott atom elektronrendszerét nem lehet akármekkora energiával gerjeszteni. Mi kell hozzá? Meghatározott energiaadag = kvantum.

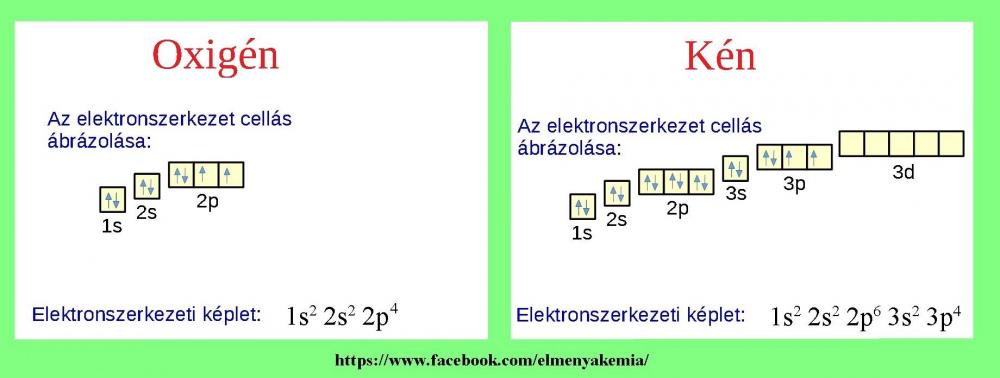
Így kell elképzelni számok tükrében az elektronszerkezet kiépülését.

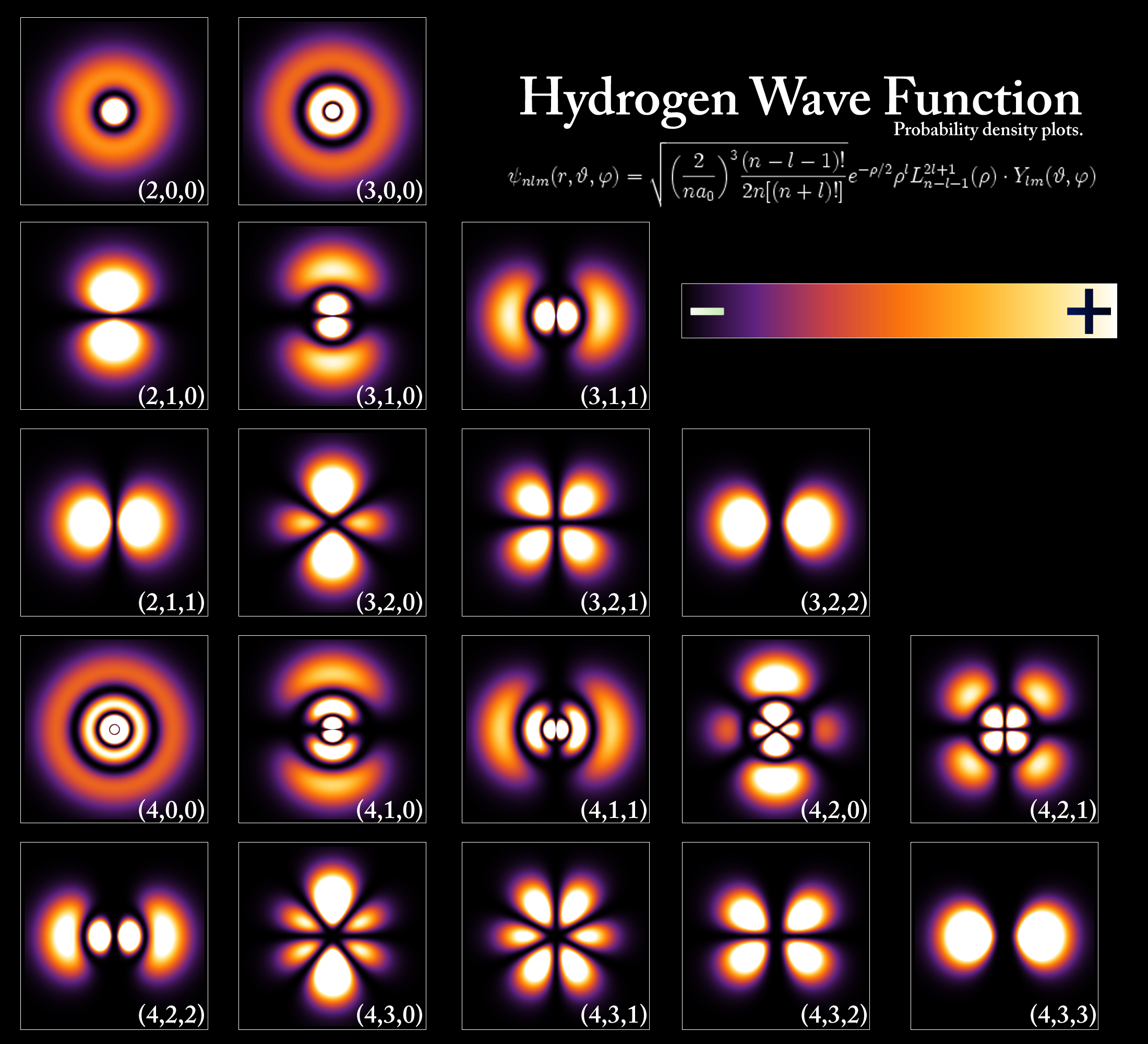
A képen látható hidrogén-valószínűségi hullám egyenlettel (komplex hullámfüggvények) tényleg kiszámítható az elektron megtalálási valószínűsége, de a világos részek is jelölik, hogy hol fordul elő legnagyobbrészt az elektron.

Héjakra, alhéjakra való beépülés:

Az elektron az energiaminimum elve alapján fog beépülni ezekre (telített alhéj esetén: max. 2 db, ellentétes spinű elektron kerülhet az atompályára).

Telítetlen alhéj esetén tud érvényesülni a Hund-szabály: a lehető legtöbb elektron párosítatlanul, azonos spinnel szeretne beépülni. Ha megfordítjuk, akkor a Hund-szabály is értelmezhetővé válik az energiaminimum elve alapján. Miért?

Az elektronok azonos negatív töltése miatt – az azonos töltések taszítják egymást. Így sokkal előnyösebb, ha távol vannak egymástól.

A nyilakat követve a pályák felépítése követhetővé válik – az elektron mindig a lehető legkisebb energiaszintű pályára akar kerülni. Amikor egy héj eléri a 8 elektronos állapotot, új elektronhéjat kezdenek feltölteni. Ennek az s-alhéja után töltődik fel az előző héj d-alhéja (3p után 4s!).